Question

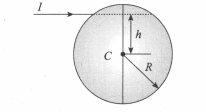
A solid sphere is placed on a horizontal plane. A horizontal impulse $l$ is applied at a distance $h$ above the central line as shown in the figure. Soon after giving the impulse, the sphere starts rolling. The ratio $\frac{h}{R}$ would be

• A. $\frac{1}{2}$
• B. $\frac{2}{5}$
• C. $\frac{1}{4}$
• D. $\frac{1}{5}$

Answer 1

Answer: (B)

Assume the sphere is rotating with angular velocity $\omega $ and moving forward with velocity $v$ . As the sphere is rolling without slipping,
$v=\omega R$
Now change in linear momentum is due to Impulse $I$ , so
$I=mv$
Also Angular momentum of the system is conserved, so about C
$\Rightarrow Ih=I_{0}\omega $ , here $I_{0}$ is moment of inertia about the center of the sphere.
$\Rightarrow mvh=\frac{2}{5}mR^{2}\omega =\frac{2}{5}mR^{2}\frac{v}{R}$
$\Rightarrow \frac{h}{R}=\frac{2}{5}$