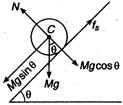
Q. A solid sphere and a hollow sphere of the same material and of a same size can be distinguished without weighing
J & K CETJ & K CET 2004
Solution:
The acceleration of a body rolling down the plane $=a$.
$\therefore a=\frac{g \sin \theta}{1+\frac{K^{2}}{R^{2}}}$
where $K$ is radius of gyration and $R$ the radius of sphere.
For solid sphere, $\frac{K^{2}}{R^{2}}=\frac{2}{5}$
$\therefore a=\frac{5}{7} g \sin \theta=0.7(g \sin \theta)$
For hollow sphere, $\frac{K^{2}}{R^{2}}=\frac{2}{3}$
$a=\frac{3}{5} g \sin \theta=0.6(g \sin \theta)$
Since, acceleration of solid sphere is more than of hollow sphere, it rolls faster, and reaches the bottom of the inclined plane earlier.
Hence, solid sphere and hollow sphere can be distinguished by rolling them simultaneously on an inclined plane.