Question

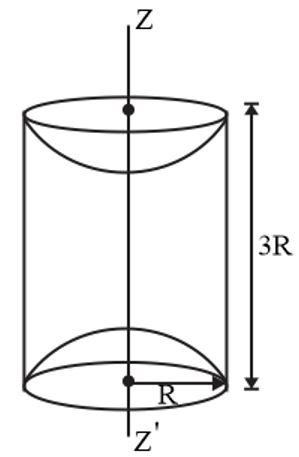
A solid cylinder is made of radius R and height 3R having mass density $\rho $ . Now two half spheres of radius R are removed from both ends. The moment of inertia of remaining portion about axis ZZ' can be calculated as $\frac{29}{6 K}\pi R^{5}\rho $ . Find K.

Answer 1

Effectively we have removed a solid sphere out of the solid cylinder.
The mass and moment of inertia of the entire cylinder are
$M_{cylinder}=\left(\pi R^{2} \times 3 R\right)\rho $
$I_{cylinder}=\frac{1}{2}\left(3 \pi R^{3} \rho \right)R^{2}$
Similarly, the mass and moment of inertia of the solid sphere are
$M_{sphere}=\frac{4}{3}\pi R^{3}\rho $
$I_{sphere}=\frac{2}{5}\left(\frac{4}{3} \pi R^{3} \rho \right)R^{2}$
$I_{remaining}=I_{cylinder}-I_{sphere}=\frac{29}{30}\pi R^{5}\rho $
$I_{remaining}=\frac{29}{6 \times 5}\pi R^{5}\rho $
$\Rightarrow K=5$