Question

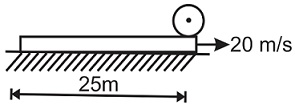
A solid cylinder is kept on one edge of a plank of same mass and length $25 \, m$ placed on a smooth surface as shown in the figure. The coefficient of friction between the cylinder and the plank is $0.5$ . The plank is given a velocity of $20 \, m \, s^{- 1}$ towards right. Find the time (in $s$ ) after which plank and cylinder will separate. [ $g=10 \, m \, s^{- 2}$ ]

Answer 1

Drawing free body diagram of the cylinder with respect to plank.
$2\,\mu mg=ma\Rightarrow a=2\,\mu g$
$\left(\mu m g R\right)=\frac{1}{2}mR^{2}\alpha \, ;\alpha -\frac{2 \mu g}{r}$
Acceleration of point of contact with respect to plank is $4\,\mu g$
Velocity of pure rolling starts,
$-v+4\mu gt=0$
$t=\frac{20}{4 \times 0.5 \times 10}=1s$
Distance traveled by cylinder with respect to plank in $1s$ is
$S'=-vt+\frac{1}{2}\left(2 \mu g\right)t^{2}=-15m$
At $t=1\,s$ , the velocity of cylinder with respect to plank is
$t=1s$
$v_{r e l}=-v+2\mu gt=-20+2\times 0.5\times 10=-10\, m/s$
Remaining $10 \,m$ will be travelled in time $t'=\frac{10}{10}=1s$
$\therefore $ Total time $= 2s$