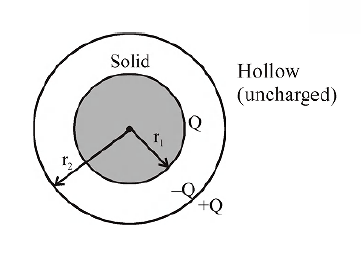
Q. A solid conducting sphere, having a charge $Q$, is surrounded by an uncharged conducting hollow spherical shell. Let the potential difference between the surface of the solid sphere and that of the outer surface o f the hollow shell be $V$. If the shell is now given a charge of $-4\, Q$, the new potential difference between the same two surfaces is :
Solution:
As given in the first condition :
Both conducting spheres are shown.
$ V_{in } - V_{out } = \left(\frac{kQ}{r_{1}} \right) - \left(\frac{kQ}{r_{2}}\right) $
$ =kQ \left(\frac{1}{r_{1}} - \frac{1}{r_{2}} \right)=V $
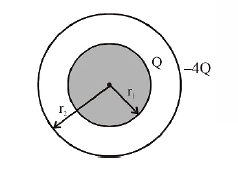
$ V_{in } -V_{out } = \left(\frac{kQ}{r_{1}} - \frac{4kQ}{r_{2}}\right) - \left(\frac{kQ}{r_{2}} - \frac{4kQ}{r_{2}}\right) $
$ = \frac{kQ}{r_{1}} - \frac{kQ}{r_{2}} $
$ = kQ \left(\frac{1}{r_{1}} - \frac{1}{r_{2}}\right) = V $
Hence, we also obtain that potential difference does not depend on charge of outer sphere.
$\therefore $ P.d. remains same