Question

A solid body X of heat capacity C is kept in an atmosphere
whose temperature is T$_A$ = 300 K. At time t = 0, the
temperature of X is T$_0$ = 400 K. It cools according to
Newton's law of cooling. At time $t_1$, its temperature is found
to be 350 K.
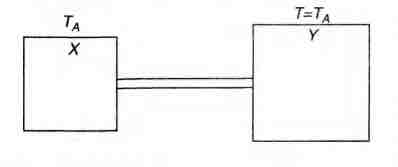
At this time (t_1,) the body X is connected to a large body Y at
atmospheric temperature T$_A$ through a conducting rod of
length L, cross-sectional area A and thermal conductivity K.
The heat capacity of Y is so large that any variation in its
temperature may be neglected. The cross-sectional area A of
the connecting rod is small compared to the surface area of X.
Find the temperature of X at time t = 3$t_1$.

Answer 1

In the first part of the question (t $\le t_1)$ At t = 0,$T_x =T_0 = 400 K and at t = t_1 T_x = T_1 = 350K$ Temperature of atmosphere, $T_A $ - 300 K (constant) This cools down according to Newton's law of cooling. Therefore, rate of cooling $$ temperature difference $\therefore \, \, \, \, \, \, \, \, \, \, bigg(-\frac{dT}{dt}\bigg)=K(T-T_A)$ $\Rightarrow \, \, \, \, \, \, \, \, \, \, \frac{dT}{T-T_A} =-k \, dt$ $\Rightarrow \, \, \, \, \, \, \, \, \, \, \int_{T_0}^{T_1} \frac{dT}{T-T_A} =-k\int_0^{t_1} dt$ $\Rightarrow \, \, \, \, \, \, \, \, \, \, ln\bigg(\frac{T_1 -T_A}{T_0 -T_A}\bigg)=-kt_1$ $\Rightarrow \, \, \, \, \, \, \, \, \, kT_1 =ln(2) \, \, \, \, \, \, \, \, \, \, \, $ .....(i) In the second part (t > t_1, \, body X cools by radiation (according to Newton's law) as well as by conduction. Therefore, rate of cooling = (cooling by radiation) + (cooling by conduction) $\therefore \, \, \, \, \, \bigg(-\frac{dT}{dt}\bigg) -k(T-T_A)+\frac{KA}{CL}(T-T_A)$ ... (ii) In conduction, $\frac{dQ}{dt}=\frac{KA(T-T_A)}{L}=C \bigg(-\frac{dT}{dt}\bigg)$ $\therefore \, \, \, \, \, \, \bigg(-\frac{dT}{dt}\bigg)=\frac{KA}{LC}(T-T_A)$ where, C = heat capacity of body X $ \, \, \, \, \, \bigg(-\frac{dT}{dt}\bigg)=\bigg(k+\frac{KA}{CL}\bigg)(T-T_A) \, \, \, \, \, \, \, \, \, \, \, $ ... (iii) Let at t = 3t$_i$, temperature of X becomes T$_2$ Then from Eq. (iii) $ \, \, \, \, \, \, \, \, \int_{T_1}^{T_2} \frac{dT}{T-T_A} =- \bigg(k+\frac{KA}{LC}\bigg) \int_{t_1}^{3t_1} dt$ $ \, \, \, \, \, \, \, \, \, \, \, ln\bigg(\frac{T_2 -T_A}{T_1 -T_A}\bigg) =-\bigg(k+\frac{KA}{LC}\bigg)(2t_1)$ $ =-\bigg(2kt_1 +\frac{2KA}{LC} t_1\bigg)$ or ln $\bigg(\frac{T_2 -300}{350-300}\bigg) = -2 ln (2) -\frac{2KAt_1}{LC}$ kt$_1$= ln(2)from Eq. (i) This equation gives $ \, \, \, \, \, \, \, \, \, T_2 =\bigg(300+12.5 e^{\frac{-2KAt_1}{CL}}\bigg) K$ .