Question

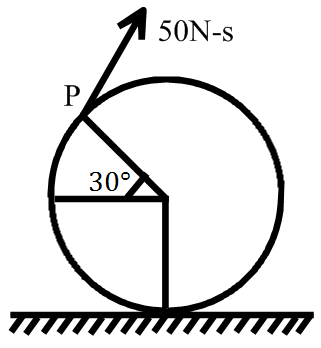
A solid ball of radius $0.2$ $ \, m$ and mass $1$ $kg$ lying at rest on a smooth horizontal surface is given an instantaneous impulse of $50$ $N \, s$ at point $P$ as shown. The number of rotations made by the ball about its diameter before hitting the ground is

• A. $\frac{625 \sqrt{3}}{2 \pi }$
• B. $\frac{2500 \sqrt{3}}{2 \pi }$
• C. $\frac{3125 \sqrt{3}}{2 \pi }$
• D. $\frac{1250 \sqrt{3}}{2 \pi }$

Answer 1

Answer: (C)

Impulse = change in momentum
Along vertical
$V_{ V }=\frac{50 \cos 30^{\circ}}{1} \frac{m}{s}=25 \sqrt{3} m s ^{-1}$
Along horizontal
$V_{H}=\frac{50 cos 60 ^\circ }{1}\frac{m}{s}=25$ $ms^{- 1}$
Time of flight $T=\frac{2 V_{V}}{g}=5\sqrt{3 }s$
Also $\omega =\frac{50 \times 0.2}{\frac{2}{5} m r^{2} \, }$ $rads^{- 1}$
$=625$ $rads^{- 1}$
$2\pi n=\omega \, T$
$\Rightarrow n=\frac{\omega T}{2 \pi }=\frac{3125 \sqrt{3}}{2 \pi }$