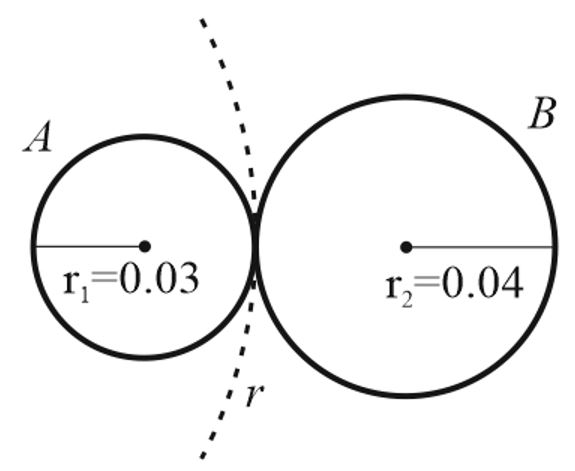
Question

A soap bubble $A$ of radius $0.03 \, m$ and another bubble $B$ of radius $0.04 \, m$ coalesce to form a combined bubble such that the radius of curvature of their common interface is $r$ . Then, the value of $r$ is

• A. $0.24\,m$
• B. $0.48\,m$
• C. $0.12\,m$
• D. none of these

Answer 1

Answer: (C)

Let the radius of curvature of the common internal film surface of the double bubble formed by two bubbles $A$ and $B$ be $r$ .

Excess of pressure as compared to the atmosphere inside $A$ is
$p_{1}=\frac{4 T}{r_{1}}=\frac{4 T}{0 .03}$
Excess of pressure inside $B$ is
$p_{2}=\frac{4 T}{r_{2}}=\frac{4 T}{0 .04}$
In the double bubble, the pressure difference between $A$ and $B$ on either side of the common surface is
$\frac{4 T}{0 .03}-\frac{4 T}{0 .04}=\frac{4 T}{r}$
$\Rightarrow \frac{1}{0 .03}-\frac{1}{0 .04}=\frac{1}{r}$
$\Rightarrow \, r=\frac{0 .03 \times 0 .04}{0 .01}=0.12\,m$