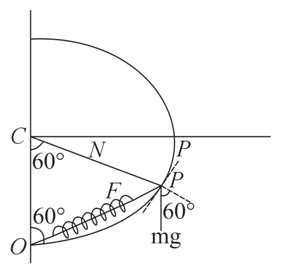
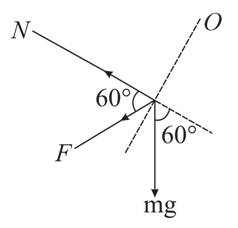
Q.
A smooth semicircular wire track of radius $R$ is fixed in a vertical plane. One end of a massless spring of natural length $\frac{3 R}{4}$ is attached to the lowest point $O$ of the wire track. A small ring of mass $m$ which can slide on the track is attached to the other end of the spring. The ring is held stationary at point $P$ such that the spring makes an angle of $60 ^\circ $ with the vertical. The spring constant $K=\frac{m g}{R}$ . Consider the instant when the ring is released. The normal reaction on the ring by the track is
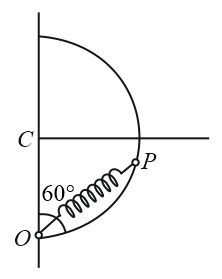
NTA AbhyasNTA Abhyas 2022
Solution: