Question

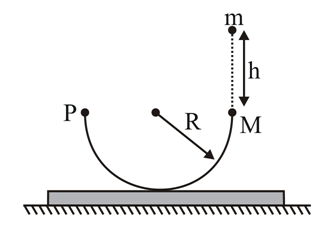
A smooth hemisphere of radius $R$ is fixed to the top of the plank which can slide freely on the smooth horizontal ground. The total mass of hemisphere and plank is $M$ and initially at rest. A particle of mass $m$ is dropped into the hemisphere tangentially from a height $h=R$ above its edge. The particle slides all the way along the inner surface of hemisphere with negligible friction. The force the ball exerts on the hemisphere at its lower most point is ...... $N$ . $\left(R = 0 . 5 \,m , M = 2\, k g , m = 0 . 5 \,kg , g = 10\, m / s^{2}\right)$

Answer 1

$mg\times \left(\right.h+R\left.\right)=\frac{1}{2}mv_{1}^{2}+\frac{1}{2}Mv_{2}^{2}$ ......(i)
$N-mg=\frac{m v_{r e l}^{2}}{R}$ ........(ii)
$v_{r e l}=v_{1}+v_{2}$ ........(iii)
$m_{1}v_{1}=M_{2}v_{2}$ .......(iv)