Q. A small spherical droplet of density $d$ is floating exactly half immersed in a liquid of density $\rho$ and surface tension $T$. The radius of the droplet is (take note that the surface tension applies an upward force on the droplet):
Solution:
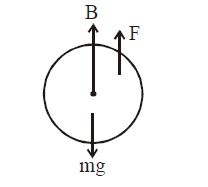
FBD of droplet
$B + F = mg$
$B = \left(\frac{2}{3}\pi R^{3}\right)\rho g$
$F = T\left(2\pi R\right)$
$m =d \left(\frac{4}{3}\pi R^{3}\right)$
$\left(\frac{2}{3}\pi R^{3}\right)\rho g + T\left(2\pi R\right) = \left(\frac{4}{3}\pi R^{3}\right)g$
$T\left(2\pi R\right) = \left(\frac{2}{3}\pi R^{3}\right)g \left[2d-\rho\right]$
$R = \sqrt{\frac{3T}{\left(2d-\rho\right)g}}$