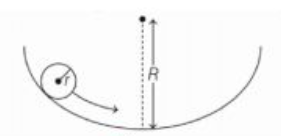
Question

A small sphere of radius $r$ is placed as a concave surface of radius of curvature $R$ a little away from the centre. When the sphere is released, it oscillates. Assuming the oscillation to be simple harmonic motion, and $r< < R$ then the time period is

• A. $2 \pi \sqrt{\frac{R}{g}}$
• B. $2 \pi \sqrt{\frac{3 R}{2 g}}$
• C. $2 \pi \sqrt{\frac{2 R}{3 g}}$
• D. $2 \pi \sqrt{\frac{R}{2 g}}$

Answer 1

Answer: (A)

The motion of sphere is as shown in figure

As, the sphere has simple harmonic motion on a curved surface,
which is equivalent to the motion of pendulum.
So, its time period is
$T=2 \pi \sqrt{\frac{I}{g}}$
Here, $l=R$
$\therefore T=2 \pi \sqrt{R / g}$