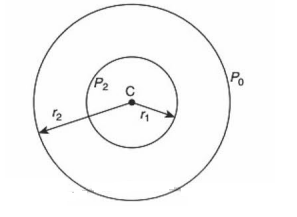
Question

A small soap bubble of radius $4\, cm$ is trapped inside another bubble of radius $6\, cm$ without any contact. Let $P_2$ be the pressure inside the inner bubble and $P_0$, the pressure outside the outer bubble. Radius of another bubble with pressure difference $P_2 - P_0$ between its inside and outside would be :

• A. 12 cm
• B. 2.4 cm
• C. 6 cm
• D. 4.8 cm

Answer 1

Answer: (B)

We know that excess pressure inside a soap bubble is $\frac{4 T}{r}$,
where $T$ is surface tensions of soap bubble and $r$ is radius of bubble.
Given: $r_{1}=4\, cm ,\, r_{2}=6\, cm$. Now,

$P_{2}=P_{0}+\frac{4 T}{r_{1}}+\frac{4 T}{r_{2}}$
$\Rightarrow P_{2}=P_{0}+4 T\left[\frac{1}{r_{1}}+\frac{1}{r_{2}}\right]$
$\Rightarrow \left(P_{2}-P_{0}\right)=4 T\left[\frac{1}{4}+\frac{1}{6}\right]$
$\Rightarrow \left(P_{2}-P_{0}\right)=4 T \frac{(3+2)}{12}$
$\Rightarrow \left(P_{2}-P_{0}\right)=4 T \times \frac{5}{12}$
$\Rightarrow \frac{4 T}{\left(\frac{12}{5}\right)}$
Let a single bubble to have this excess pressure has radius $r$.
Therefore, on comparison
$\frac{4 T}{r}=\frac{4 T}{\frac{12}{6}}$
$\Rightarrow r=\frac{12}{5}=2.4\, cm$