Question

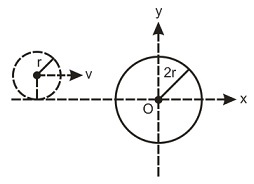
A small smooth disc of mass $m$ and radius $r$ moving with an initial velocity $v$ along the positive $x$ -axis collided with a big disc of mass $2m$ and radius $2r$ which was initially at rest with its centre at origin as shown in the figure. If the coefficient of restitution is $0$ , then the velocity of the larger disc after the collision is

• A. $\frac{8}{27}\text{v }\hat{i}-\frac{2 \sqrt{2}}{27}\text{v }\hat{j}$
• B. $\frac{8}{27}\text{v }\hat{i}-\frac{\sqrt{2}}{27}\text{v }\hat{j}$
• C. $\frac{\text{v}}{3}\hat{i}$
• D. $\frac{2 \sqrt{2}}{27}\text{v }\hat{i}-\frac{8}{27}\text{v }\hat{j}$

Answer 1

Answer: (A)

The larger disc will move along line of impact
As $e=0$ , so velocity of larger disc
$\text{v}^{'} = \frac{\text{mv cos } \theta }{\text{m} + 2 \text{m}} = \frac{\text{v cos } \theta }{3}$
Velocity of larger disc
$=\text{v}^{'}\text{cos }\theta \, \hat{i}-\text{v}^{'}\text{sin }\theta \, \hat{j}$
$=\frac{\text{v}}{3}\text{cos}^{2}\theta \hat{i}-\frac{\text{v}}{3}\text{sin}\theta \text{cos }\theta \, \hat{j}$
( from the figure we can calculate $cos\theta =\frac{2 \sqrt{2}}{3}$ , $sin\theta =\frac{1}{3}$ )
$=\frac{8}{27}\text{v }\hat{i}-\frac{2 \sqrt{2}}{27}\text{v }\hat{j}$