Question

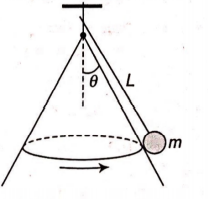
A small sized mass $m$ is attached by a massless string (of length L) to the top of a fixed frictionless solid cone whose axis is vertical. The half angle at the vertex of the cone is $\theta$ If the mass $m$ moves around in a horizontal circle at speed $v$, what is the maximum value of $v$ for which mass stays in contact with the cone? (g is acceleration due to gravity)

• A. $\sqrt{gL\,cos\,\theta}$
• B. $\sqrt{gL\,sin\,\theta}$
• C. $\sqrt{gL\,sin\,\theta\,tan\,\theta}$
• D. $\sqrt{gL\,tan\,\theta}$

Answer 1

Answer: (C)

At maximum velocity the mass will just loose contact with cone and will behave like free conical pendulum with time period
$T=2\pi \sqrt{\frac{L\,cos\,\theta}{g}} $
$\Rightarrow \omega=\frac{2\pi}{T} \sqrt{\frac{g}{L\,cos\,\theta}}$
Hence $V_{\text{max}} =\left(L\,sin \,\theta\right) \omega$
$=\sqrt{gL\,sin\,\theta\,tan\,\theta}$