Question

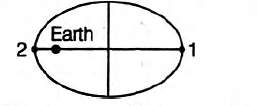
A small satellite is in elliptical orbit around the earth as shown in figure. $ L $ denotes the magnitude of its angular momentum and $ K $ denotes its kinetic energy. If $ 1 $ and $ 2 $ denote two positions of the satellite, then

• A. $ L_{2} = L_{1} $ , $ k_{2} = k_{1} $
• B. $ L_{2} = L_{1} $ , $ k_{2} > \, k_{1} $
• C. $ L_{2} > \, L_{1} $ , $ k_{2} < \, k_{1} $
• D. $ L_{2}= L_{1} $ , $ k_{2} < \, k_{1} $

Answer 1

Answer: (B)

By Kepler's law, when a satellite is moving around the earth on elliptical path, then its angular momentum remains constant
i.e. $L_{1}=L_{2}$
$m_{1}v_{1}r_{1}=m_{2}v_{2}r_{2}$
But, $m_{1}=m_{2}=m$
$\therefore v_{1}r_{1}=v_{2}r_{2}$
$\frac{r_{1}}{r_{2}}=\frac{v_{2}}{v_{1}}\ldots\left(i\right)$
Here, $r_{1}>\,r_{2}$
$\frac{r_{1}}{r_{2}}>\,1$
$\therefore $ From Eq. $\left(i\right)$,
$\frac{v_{2}}{v_{1}}>\,1$
$v_{2}>\,v_{1}$
$v_{2}^{2}>\,v_{1}^{2}$ or $\frac{1}{2}mv_{2}^{2}>\,\frac{1}{2}mv_{1}^{2}$
$K_{2}>\,K_{1}$ $(\because K=\frac{1}{2}mv^{2})$