Q.
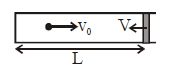
A small particle of mass m moving inside a heavy, hollow and straight tube along the tube axis undergoes elastic collision at two ends. The tube has no friction and it is closed at one end by a flat surface while the other end is fitted with a heavy movable flat piston as shown in figure. When the distance of the piston from closed end is L = L0 the particle speed is v = v0. The piston is moved inward at a very low speed V such that V << $\frac{dL}{L}$ V0 , where dL is the infinitesimal displacement of the piston. Which of the following statement(s) is/are correct ?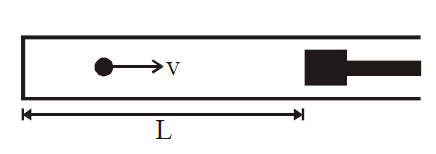
Solution:
(1) average rate of collision = $\frac{2L}{v}$
(2) speed of particle after collision $= 2V + v_{0}$
change in speed $= \left(2V + v_{0}\right) - v_{0}$
after each collision = 2V
no. of collision per unit time (frequency) $= \frac{v}{2L}$
change in speed in dt time $= 2V ×$ number of collision in dt time
$\Rightarrow \,dv = 2V \left(\frac{v}{2L}\right). \frac{dL}{V}$
$dv = \frac{vdL}{L}$
Now, $dv = - \frac{vdL}{L}$ {as L decrease}
$\int\limits^{v}_{v_0} \frac{dv}{v} = - \int\limits^{L_{0}/2}_{L_0} \frac{dL}{L}$
$\Rightarrow \,\left[ln \,v\right]^{v}_{v_0} = -\left[ln\,L\right]^{L_{0}/2}$
$\Rightarrow \,v = 2v_{0}$
$\Rightarrow \,KE_{L_0} = \frac{1}{2}mv^{2}_{0}\quad\quad \frac{KE_{L_0/2}}{KE_{0}} = 4$
$KE_{L_0/2} = \frac{1}{2}m\left(2v_{0}\right)^{2}$
or
$\left(dt\right)\left(\frac{v}{2x}\right) \frac{2mv}{dt} = F$
$F = \frac{mv^{2}}{x}$
$-m\,v \frac{dv}{dx} = \frac{mv^{2}}{x}$
$- \frac{dv}{v} = \frac{dx}{x}$
$ln \frac{v_{2}}{v_{1}} =ln \frac{x_{1}}{x_{2}}$
vx = constant $\Rightarrow $ on decreasing length to half K.E. becomes 1/4
$vdx + xdv = 0$