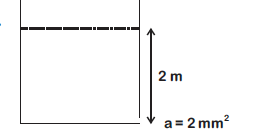
Q. A small hole of area of cross-section $2 \,mm^2$ is present near the bottom of a fully filled open tank of height $2 \,m$. Taking $g = 10 \,m/s^{-2}$. the rate of flow of water through the open hole would be nearly:
Solution:
Rate of flow liquid
$Q =au = a\sqrt{2gh} $
$ =2\times10^{-6} m^{2} \times\sqrt{2\times10\times2} m/s $
$= 2\times2 \times3.14 \times10^{-6} m^{3}/s ^{-1}$
$ = 12.56\times10^{-6} m^{3}/s ^{-1}$
$= 12.6 \times10^{-6} m^{3} /s ^{-1}$