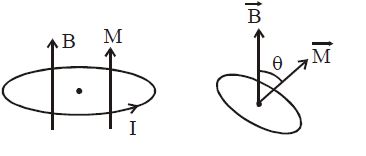
Q. A small circular loop of conducting wire has radius a and carries current $I$. It is placed in a uniform magnetic field $B$ perpendicular to its plane such that when rotated slightly about its diameter and released, it starts performing simple harmonic motion of time period $T$. If the mass of the loop is $m$ then :
Solution:
$\vec{T} = \vec{M} \times \vec{B} = -MBsin\theta$
$I\alpha = -MB\,sin\theta$
for small $\theta$,
$\alpha = -\frac{MB}{I} \theta$
$\omega = \sqrt{\frac{MB}{I}} = \sqrt{\frac{\left(i\right)\left(\pi R^{2}\right)B}{\left(\frac{mR^{2}}{2}\right)}}$
$\omega = \sqrt{\frac{2i\pi B}{m}}$
$\therefore = T = \frac{2\pi}{\omega} = \sqrt{\frac{2i\pi B}{iB}}$