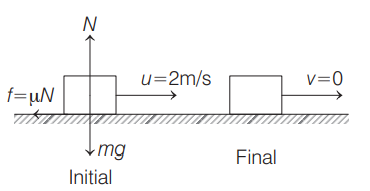
Question

A small body of mass $500\, g$ moves on a rough horizontal surface before finally stops. The initial velocity of the body is $2\, m / s$ and coefficient of friction is $0.3$. Then, find absolute value of the average power developed by the frictional force during the time of motion. (Take, $g=10\, m / s ^{2}$ )

• A. 1 W
• B. 1.5 W
• C. 2 W
• D. 2.5 W

Answer 1

Answer: (B)

As, retardation is constant, so average velocity
$v_{ av }=\frac{u+v}{2}=\frac{2+0}{2}=1\, m / s$
Now, friction force, $f=\mu N=\mu mg$
Given, coefficient of friction, $\mu=0.3$
Mass of body, $m=500\, g =0.5\, kg$
$\Rightarrow f=0.3 \times 0.5 \times 10$
$f=1.5\, N$
Average power by friction,
$P_{ av }=f v_{ av }$
$P_{ av }=1.5 \times 1=1.5\, W$