Question

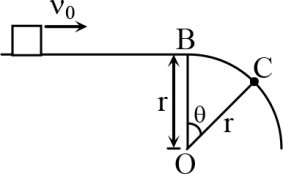
A small block slides with velocity $0.5 \, \sqrt{g r}$ on the horizontal frictionless surface as shown in the figure. The block leaves the surface at a point $C$ . The value of $\cos\theta =\frac{x}{4}$ , find $x$ .

Answer 1

$m g \cos \theta-N=\frac{m v^{2}}{r} ; N=m g \cos \theta-\frac{m v^{2}}{r}$
$N=0 \Rightarrow m g \cos \theta=\frac{m v^{2}}{r}$
$v=\sqrt{g r \cos \theta}$ or $\cos \theta=\frac{v^{2}}{g r}$....(i)
Now, from the conservation of energy, we have,
$\frac{m v_{0}^{2}}{2}+m g r(1-\cos \theta)=\frac{m v^{2}}{2} \ldots 2$
Substituting the value of $m v^{2}$ from equation 1 in equation 2 ,
$\frac{m v_{0}^{2}}{2}+m g r(1-\cos \theta)=\frac{m g r \cos \theta}{2} $
$\Rightarrow m g r(1-\cos \theta)=\frac{m g r \cos \theta}{2}-\frac{m 0.5 \sqrt{g r}^{2}}{2}$
$\Rightarrow 1-\cos \theta=\frac{\cos \theta}{2}-\frac{1}{8} $
$\Rightarrow \cos \theta=\frac{3}{4}$
Thus, $x=3$.