Question

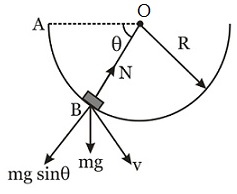
A small block of mass $\text{m}$ is released from rest from point $\text{A}$ inside a smooth hemisphere bowl of radius $\text{R}$ , which is fixed on ground such that $\text{OA}$ is horizontal. The ratio $\text{(x)}$ of magnitude of centripetal force and normal reaction on the block at any point $\text{B}$ varies with $\theta $ as:

• A.
  
  
• B.
  
  
• C.
  
  
• D.
  
  

Answer 1

Answer: (A)

$\frac{m v^{2}}{R}=N-mgsin \theta $
$N=\frac{m v^{2}}{R}+mgsin \theta $

By energy conservation,
$mgR \, sin\theta =\frac{1}{2}mv^{2}$
$\frac{m v^{2}}{R}=2mgsin \theta $
$N=3mgsin \theta $
$Ratio=\frac{m v^{2}}{R N}=\frac{2}{3}$ (constant)
$x=\frac{2}{3}$