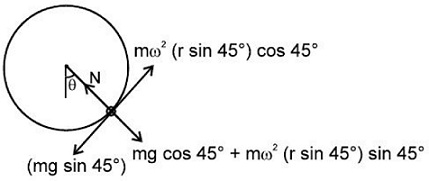Question

A small bead of mass $m=1 \, kg$ is free to move on a circular hoop. The circular hoop has centre at $C$ and radius $ \, r=1 \, m$ and it rotates about a fixed vertical axis. The coefficient of friction between bead and hoop is $\mu =0.5$ . The maximum angular speed of the hoop for which the bead does not have relative motion with respect to the hoop, at the position shown in the figure is: (Take $g=10 \, m \, s^{- 2}$ )

• A. $\left(5 \sqrt{2}\right)^{\frac{1}{2}}$
• B. $\left(10 \sqrt{2}\right)^{\frac{1}{2}}$
• C. $\left(15 \sqrt{2}\right)^{\frac{1}{2}}$
• D. $\left(30 \sqrt{2}\right)^{\frac{1}{2}}$

Answer 1

Answer: (D)

The maximum angular speed of the hoop corresponds to the situation when the bead is just about to slide upwards.
The free-body diagram of the bead is

For the bead not to slide upwards
$m \omega^2\left(r \sin 45^{\circ}\right) \cos 45^{\circ}-m g \sin 45^{\circ}<\mu N \ldots$ ...(i)
Where $N=m g \cos 45^{\circ}+m \omega^2\left(r \sin 45^{\circ}\right) \sin 45^{\circ} \ldots$ ...(ii)
From (i) and (ii) we get,
$\omega =\sqrt{30 \sqrt{2}}$ $rads^{- 1}$