Question

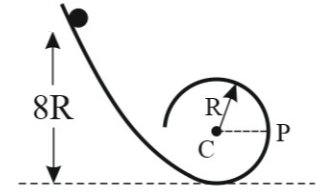
A small ball of mass $m$ and radius $r=\frac{R}{10}$ rolls without slipping along the track shown in the figure. The radius of circular part of the track is $R$ . If the ball starts from rest at a height of $8R$ above the bottom, the normal force on the ball at the point $P$ is

• A. $\frac{100}{3}mg$
• B. $\frac{100}{9}mg$
• C. $\frac{200}{9}mg$
• D. $\frac{50}{7}mg$

Answer 1

Answer: (B)

Using Work-Energy Theorem
$7mgR=\frac{1}{2}\left(mv\right)^{2}+\frac{1}{2}\left(\frac{2}{5} \left(mr\right)^{2}\right)\times \left(\omega \right)^{2}$
since the sphere is rolling without slipping $v=rω$
$\therefore 7mgR=\frac{1}{2}\times \, \left(\frac{7}{5} \left(mr\right)^{2}\right)\times \, \frac{v^{2}}{r^{2}}$
$\Rightarrow v^{2}=10gR$
at point $P$ , we can consider sphere as a point object doing circular motion in a circle of the radius $\left(\right.R-r\left.\right)$ with velocity $v$ ,
Hence at point $P$
$N=\frac{\left(mv\right)^{2}}{\left(R - r\right)}=\frac{10 mgR}{\left(R - \frac{R}{10}\right)}=\frac{10 mgR}{\frac{9 R}{10}}$ ( given $r=\frac{R}{10}$ )
or $N=\frac{100}{9}mg$