Q.
A small ball is to be thrown, so as to just pass through three equal rings of diameter $2 \,m$ and placed in parallel vertical planes at distance $8\, m$ apart with their highest points at height $32 \,m$ above the point of projection as shown in the figure. If the angle of projection with horizontal is $\alpha$. The value of $\tan \alpha$ is _____.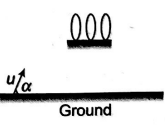
Motion in a Plane
Solution:
