Q.
A sinusoidal wave moving along a string is shown twice in the figure, as crest $A$ travels in the positive direction of an $x$ axis by distance $d=6.0\, cm$ in $4.0\, m$. The tick marks along the axis are separated by $10\, cm$; height $H=6.00\, mm$. The wave equation is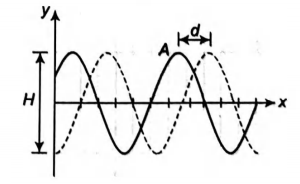
Waves
Solution: