Question

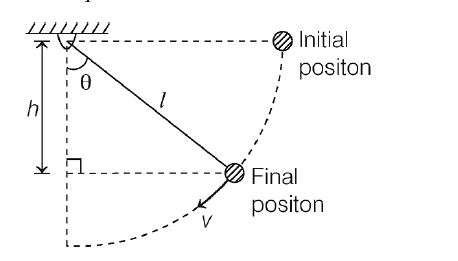
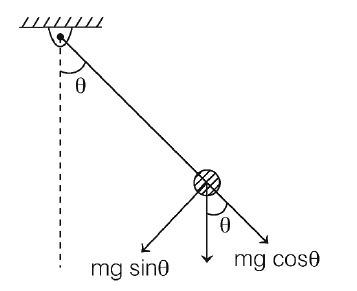
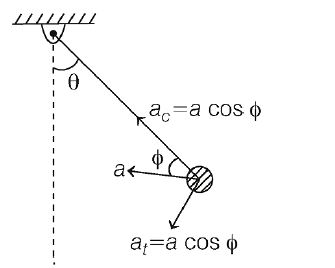
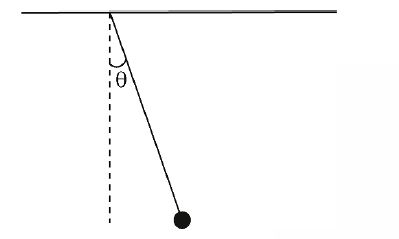
A simple pendulum is released from re stat the horizontally stretched position. When the string makes an angle $\theta$ with the vertical, the angle which the acceleration vector of the bob makes with the string is given by

• A. $\phi=0$
• B. $\phi=\tan ^{-1}\left(\frac{\tan \theta}{2}\right)$
• C. $\phi=\tan ^{-1}\left(2 \tan \theta\right)$
• D. $\phi=\frac{\pi}{2}$

Answer 1

Answer: (B)

Let $v$ is the velocity of bob at position $\theta$ after being released from $\theta$ horizontal position

From energy conservation, we have
$m g h=\frac{1}{2} m v^{2}$
$\Rightarrow m g(l \cos \theta)=\frac{1}{2} m v^{2}$
$\Rightarrow \frac{v^{2}}{l}=2 g \cos \theta\,\,\,...(i)$
Restoring force on bob is component of weight.

So, tangential component of acceleration is
$a_{t} =g \sin \theta \ldots\left(ii\right) $
If total acceleration a makes angle $\phi$ with string. Then,

Tangential component
$a_{t}=a \sin \phi$
and radial component, $a_{c}=a \cos \phi$
So, $\frac{a_{t}}{a_{c}}=\frac{a \sin \phi}{a \cos \phi}=\tan \phi$
$\Rightarrow \tan \phi \frac{a_{t}}{a_{c}} \ldots\left(iii\right)$
Substituting values of $a_{t}$ and $a_{c}$ from Eqs.
(i) and (ii) in Eq. (iii), we get
$\tan \phi =\frac{g \sin \theta }{2g \cos \theta}$
$\Rightarrow \tan \phi=\frac{\tan \theta}{2}$
so, $\phi=\tan ^{-1} \left(\frac{\tan \theta}{2}\right)$