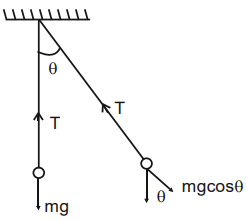
Q. A simple pendulum, consisting of a small ball of mass $m$ attached to a massless string hanging vertically from the ceiling, is oscillating with an amplitude such that $T_{\max }=2 T_{\min }$ where $T_{\max }$ and $T_{\min }$ are the maximum and minimum tension in the string respectively. The value of maximum tension $T_{\max }$ in the string is
WBJEEWBJEE 2021
Solution: