Question

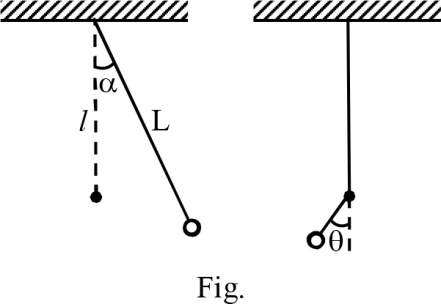
A simple pendulum consisting of a mass $M$ attached to a string of length $L$ is released from rest at an angle $\alpha $ . A pin is located at a distance $l$ below the pivot point. When the pendulum swings down, the string hits the pin as shown in the figure. If the particle doesn't undergo a complete vertical circle, then the maximum angle $\theta \, \left( < \left(\pi \right)/2\right)$ through which the string swings after hitting the pin is

• A. $cos^{- 1} \left[\frac{L cos ⁡ \alpha + l \, }{L + l}\right]$
• B. $cos^{- 1} \left[\frac{L cos ⁡ \alpha - l \, }{L - l}\right]$
• C. $cos^{- 1} \left[\frac{L cos ⁡ \alpha + l \, }{L - l}\right]$
• D. $cos^{- 1} \left[\frac{L cos ⁡ \alpha - l \, }{L + l}\right]$

Answer 1

Answer: (B)

At the bottom most point, square of speed of bob,
$v^{2}=2gL\left(1 \, - \, c o s \, \alpha \right)$
It will rise further to a height,
$h=\frac{v^{2}}{2 g}= \, L\left(1 - cos \alpha \right)$
or $\left(L - l\right) \, \left(1 - cos \theta \right)=L\left(1 - cos ⁡ \alpha \right)$
$\therefore \, \theta =cos^{- 1} \left[\frac{L cos ⁡ \alpha - l}{L - l}\right]$