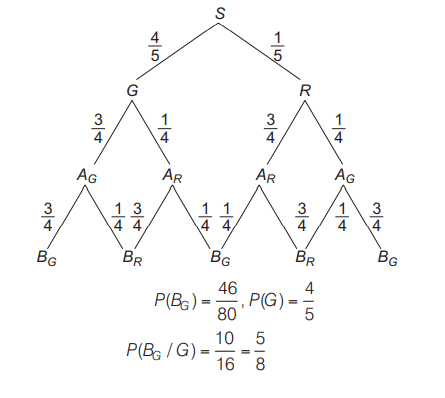
Q. A signal which can be green or red with probability $4 / 5$ and $1 / 5$ respectively, is received by station $A$ and then transmitted to station $B$. The probability of each station receiving the signal correctly is $3 / 4$. If the signal received at station $B$ is given, then the probability that the original signal is green, is
Probability - Part 2
Solution: