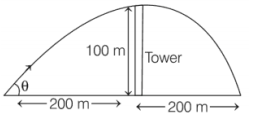
Question

A shot is fired from a point at a distance of $400\, m$, from the foot of a tower $100\, m$ high, so that it just passes over it. The direction of shot with respect to the horizontal is:

• A. $30^{\circ}$
• B. $60^{\circ}$
• C. $70^{\circ}$
• D. $45^{\circ}$

Answer 1

Answer: (D)

According to question, the given situation is shown in the figure.

Here, range, $R=200+200=400\, m$
Maximum height, $H=100\, m$
If $\theta$ be the direction of shot with respect to horizontal, then
$R=\frac{u^{2} \sin 2 \theta}{g}$ and $H=\frac{u^{2} \sin ^{2} \theta}{2 g}$
$\therefore \frac{R}{H}=\frac{\frac{u^{2} \sin 2 \theta}{g}}{\frac{u^{2} \sin ^{2} \theta}{2 g}}$
$\Rightarrow \frac{400}{100}=\frac{2 \sin 2 \theta}{\sin ^{2} \theta}$
$\Rightarrow 4=\frac{2 \times 2 \sin \theta \cos \theta}{\sin ^{2} \theta}[\because \sin 2 \theta=2 \sin \theta \cos \theta]$
$\Rightarrow 1=\tan \theta$
$\Rightarrow \tan 45^{\circ}=\tan \theta$
$\Rightarrow 45^{\circ}=\theta$
$\Rightarrow \theta=45^{\circ}$