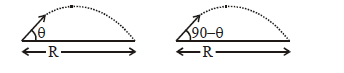Q. A shell is fired from a fixed artillery gun with an initial speed $u$ such that it hits the target on the ground at a distance $R$ from it. If $t_1$ and $t_2$ are the values of the time taken by it to hit the target in two possible ways, the product $t_1 t_2$ is:
Solution:
Range will be same for time $t_1$ & $t_2$, so angles of projection will be $'\theta'$ & $'90^{\circ} - \theta $'
$t_{1 } = \frac{2u \sin\theta}{g} t_{2} = \frac{2u \sin\left(90^{\circ} -\theta\right)}{g}$
and $ R = \frac{u^{2} \sin 2\theta}{g}$
$ t_{1}t_{2} = \frac{4u^{2} \sin\theta \cos\theta}{g^{2}} = \frac{2}{g} \left[\frac{2u^{2} \sin\theta \cos\theta}{g}\right] $
$ a= \frac{2R}{g} $