Q.
A series $R C$ circuit is formed using a resistance $R$, a capacitor without dielectric having a capacitance $C=2\, F$ and a battery of emf $E=3\, V$. The circuit is completed and it is allowed to attain the steady state. After this, at $t=0$, half the thickness of the capacitor is filled with a dielectric of constant $K=2$ as shown in the figure. The system is again allowed to attain a steady state. What will be the heat generated (in joule) in the capacitor between $t=0$ and $t=\infty$ ?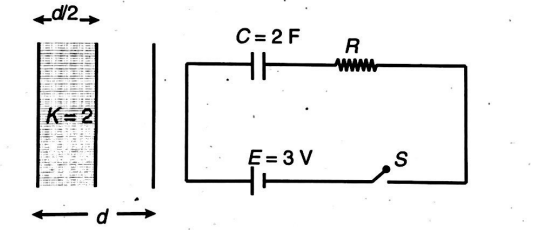
Current Electricity
Solution: