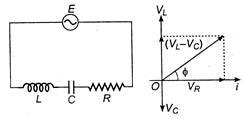
Question

A series LCR circuit is tuned to resonance. The impedance of the circuit at resonance is :

• A. $\left[R^{2}+\left(\omega L-\frac{1}{\omega C}\right)^{2}\right]^{1 / 2}$
• B. $\left[R^{2}+(\omega L)^{2}+\left(\frac{1}{\omega C}\right)^{2}\right]^{1 / 2}$
• C. $\left[R^{2}+\left(\frac{1}{\omega C}\right)^{2}\right]^{1 / 2}$
• D. $R$

Answer 1

Answer: (D)

In a series L-C-R circuit, the impedance $Z$ is given by
$Z=\sqrt{R^{2}+\left(\omega L-\frac{1}{\omega C}\right)^{2}}$
At resonance Inductive reactance $=$ capacitance reactance
$\therefore X_{L}=X_{C}$
$\Rightarrow \omega L=\frac{1}{\omega C}$ and $\tan \phi=0$,
i.e., $\phi=0$, the emf and current are in phase.
$\therefore Z=\sqrt{R^{2}+0}=R$
which is the minimum value $Z$ can have.