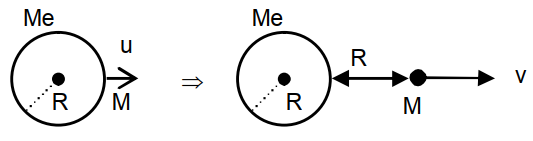
Question

A satellite of mass $M$ is launched vertically upwards with an initial speed $u$ from the surface of the earth. After it reaches height $R$ ( $R=$ radius of the earth), it ejects a rocket of mass $\frac{M}{10}$ so that subsequently the satellite moves in a circular orbit. The kinetic energy of the rocket is ( $G$ is the gravitational constant; $M_{e}$ is the mass of the earth):

• A. $\frac{M}{20}\left(u^{2} + \frac{113}{200} \frac{G M_{e}}{R}\right)$
• B. $5M\left(u^{2} - \frac{119}{200} \frac{G M_{e}}{R}\right)$
• C. $\frac{3 M}{8}\left(u + \sqrt{\frac{5 G M_{e}}{6 R}}\right)^{2}$
• D. $\frac{M}{20}\left(u - \sqrt{\frac{2 G M_{e}}{3 R}}\right)^{2}$

Answer 1

Answer: (B)

$\frac{- GM_{e} M}{R}+\frac{1}{2}Mu^{2}=\frac{- GM_{e} M}{2 R}+\frac{1}{2}Mv^{2}$

$v=\sqrt{u^{2} - \frac{G M_{e}}{R}}$
$V_{\tau} \rightarrow $ Transverse velocity of rocket
$V_{R} \rightarrow $ Radial velocity of rocket
$V=\sqrt{\frac{G M_{e}}{2 R}}$
$\frac{M}{10}V_{T}=\frac{9 M}{10}\sqrt{\frac{G M_{e}}{2 R}}$
$\frac{M}{10}V_{r}=M\sqrt{u^{2} - \frac{GM_{e}}{R}}$
Kinetic energy $=\frac{1}{2}\frac{M}{10}\left(V_{T}^{2} + V_{r}^{2}\right)=\frac{M}{20}\left(81 \frac{\left(GM\right)_{e}}{2 R} + 100 u^{2} - 100 \frac{\left(GM\right)_{e}}{R}\right)$
$=\frac{M}{20}\left(100 u^{2} - \frac{119 G M_{e}}{2 R}\right)$
$=5M\left(u^{2} - \frac{119 \left(GM\right)_{e}}{200 R}\right)$