Question

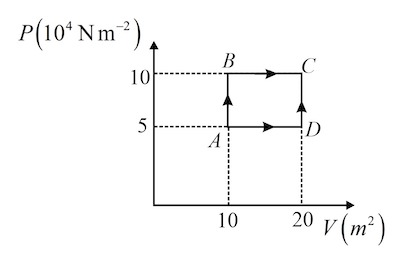
A sample of $2kg$ monoatomic helium gas (assumed ideal) is taken through the process $ABC$ and another sample of $2kg$ of the same gas is taken through the process $ADC$ . Given that the molecular mass of helium = $4amu$ , find the temperature of helium in the state $D$ . $\left[\right.$ Take the universal gas constant $R=\frac{25}{3}Jmol^{- 1}K^{- 1}\left]\right.$

Answer 1

Number of gram moles of He, $n=\frac{m}{M}=\frac{2 \times 10^{3}}{4}=500$ mole
$ \begin{array}{l} V _{ A }=10 m ^{3}, P _{ A }=5 \times 10^{4} N / m ^{2} \\ T_{A}=\frac{P_{A} V_{A}}{n R}=\frac{(10)\left(5 \times 10^{4}\right)}{(500)\left(\frac{25}{3}\right)} K =120 K \end{array} $
Similarly, $V_{B}=10 m^{3}, P_{B}=10 \times 10^{4} N / m ^{2}$
$ T_{B}=\frac{(10)\left(10 \times 10^{4}\right)}{(500)\left(\frac{25}{3}\right)} K =240 K $
Similarly, $V_{C}=20 m ^{3}, P_{C}=10 \times 10^{4} N / m ^{2}$
$ T_{C}=\frac{(20)\left(10 \times 10^{4}\right)}{(500)\left(\frac{25}{3}\right)} K =480 K $
Similarly, $V_{D}=20 m ^{3}, P_{D}=5 \times 10^{4} N / m ^{2}$
$ T_{D}=\frac{(20)\left(5 \times 10^{4}\right)}{(500)\left(\frac{25}{3}\right)} K =240 K $