Q.
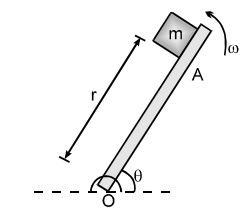
A rough platform $OA$ rotates in a vertical plane about a horizontal axis through the point $O$ with a constant counterclockwise velocity $\omega =3 \, rad \, s^{- 1}$ . As it passes through the position $\theta =0$ , a small mass $m$ is placed upon it at a radial distance. If the mass is observed to slip at $\theta =37^\circ $ , then the coefficient of friction between the mass & the member is ( consider $r=0.5 \, m$ and $g=10 \, m \, s^{- 2}$ )
NTA AbhyasNTA Abhyas 2022
Solution: