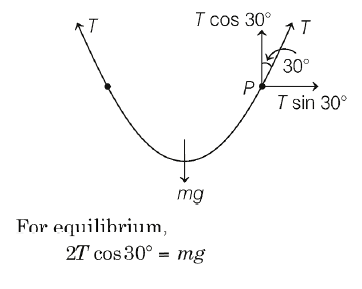
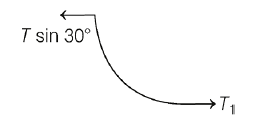
Q.
A rope of mass $5\, kg$ is hanging between two supports as shown alongside. The tension at the lowest point of the rope is close to (take, $g = 10\, m /s^2)$
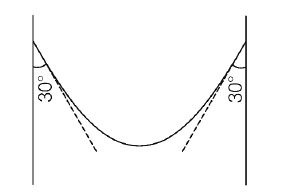
KVPYKVPY 2017
Solution:

Solution: