1. Tardigrade
  2. Question
  3. Physics
  4. A rope of mass 0.1 kg is connected at the same height of two opposite walls. It is allowed to hang under its own weight. At [he contact point between the rope and the wall, the rope makes an angle θ =10° with respect to horizontal. The tension in the rope at its midpoint between the walls is

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

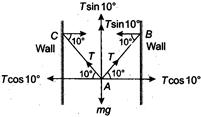
Q. A rope of mass $0.1\, kg$ is connected at the same height of two opposite walls. It is allowed to hang under its own weight. At [he contact point between the rope and the wall, the rope makes an angle $ \theta =10^{\circ} $ with respect to horizontal. The tension in the rope at its midpoint between the walls is

Delhi UMET/DPMTDelhi UMET/DPMT 2009

Solution:

Let the tension in each section $A B$ and $A C$ be $T$.
Now, from the condition of equilibrium it is clear that the horizontal components are equal in magnitude and opposite to each other so they cancel out each other.
Hence, $m g=2 T \sin 10^{\circ} $
$\therefore $ $T=\left[\frac{m g}{2 \sin 10^{\circ}}\right]$
$=\frac{0.1 \times 9.8}{2 \times 0.1736}=2.82 \,N$

Solution Image