Q.
A rolling wheel of $12\, kg$ is on an inclined plane at position $P$ and connected to a mass of $3\, kg$ through a string of fixed length and pulley as shown in figure. Consider $PR$ as friction free surface. The velocity of centre of mass of the wheel when it reaches at the bottom $Q$ of the inclined plane $P Q$ will be $\frac{1}{2} \sqrt{ xgh } m / s$. The value of $x$ is ______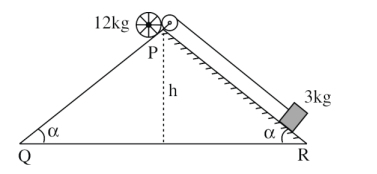
Solution: