Q.
A rod of mass $m$ and length $L$, pivoted at one of its ends, is hanging vertically. A bullet of the same mass moving at speed $v$ strikes the rod horizontally at a distance $x$ from its pivoted end and gets embedded in it. The combined system now rotates with angular speed $\omega$ about the pivot. The maximum angular speed $\omega_{M}$ is achieved for $x=x_{M}$. Then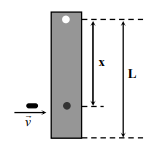
JEE AdvancedJEE Advanced 2020
Solution: