Q.
A rod of length $L$ leans against a smooth vertical wall while its other end is on a smooth floor. The end that leans against the wall moves uniformly vertically downward. Select the correct alternative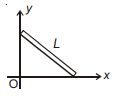
System of Particles and Rotational Motion
Solution:
Using constraint motion relation $V \cos \theta=v \sin \theta$ $V=v \tan \theta$ As $\theta$ keeps on decreasing, tan $\theta$ will also decrease and at last $\theta$ will become zero and $V=0$,
