Q.
A rod of length $l$ is placed along x-axis. One of its ends is at the origin. The rod has a non-uniform charge density $\lambda =\frac{a}{x}$ , a being a positive constant. The electric potential at the point $P$ (origin) as shown in the figure is
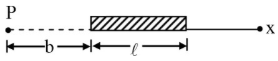
NTA AbhyasNTA Abhyas 2020Electrostatic Potential and Capacitance
Solution:
