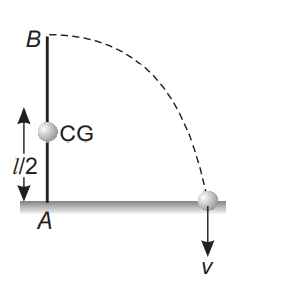
Question

A rod of length $l$ is held vertically stationary with its lower end located at a point $P$, on the horizontal plane. When the rod is released to topple about $P$, the velocity of the upper end of the rod with which it hits the ground is

• A. $\sqrt{\frac{g}{l}}$
• B. $\sqrt{3gl}$
• C. $3\sqrt{\frac{g}{l}}$
• D. $\sqrt{\frac{3g}{l}}$

Answer 1

Answer: (B)

In this process potential energy of the metre stick will be converted into rotational kinetic energy.
PE of metre stick $=\frac{m g l}{2}$ Because its centre of gravity lies at the middle of the rod.
Rotational kinetic energy $E=\frac{1}{2} I \omega^{2}$
$I=$ moment of inertia of metre stick about point $A=\frac{m l^{2}}{3}$
By the law of conservation of energy
$m g\left(\frac{l}{2}\right)=\frac{1}{2} I \omega^{2}=\frac{1}{2} \frac{m l^{2}}{3}\left(\frac{v_{B}}{l}\right)^{2}$
By solving, we get $v_{B}=\sqrt{3 g l}$