Question

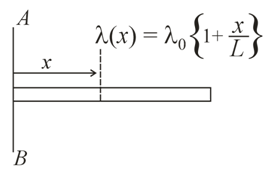
A rod of length $'L'$ has variable mass density, $\lambda \left(\right.x\left.\right)=\left(\lambda \right)_{0}\left(1 + \frac{x}{L}\right).$ There exists an axis parallel to $AB$ about which the moment of inertia of the rod is minimum. If the distance of such an axis from $AB$ is of the form $\frac{5 L}{ N},$ then find $N.$

Answer 1

Moment of inertia is minimum about an axis passing through $COM.$
$x_{ cm }=\frac{\int x d m}{\int d m}=\frac{\int\limits_{0}^{L} \lambda_{0}\left(1+\frac{x}{L}\right) x d x}{\int\limits_{0}^{L} \lambda_{0}\left(1+\frac{x}{L}\right) d x}=\frac{5 L}{9}$