Question

A rod of length $L$ and mass $M$ is acted on by two unequal forces $F_{1}$ and $F_{2}\left(<\,F_{1}\right)$ as shown in the figure.


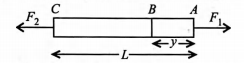
The tension in the rodata distance $y$ from the end $A$ is given by

• A. $F_{1}\left(1-\frac{y}{L}\right)+F_{2}\left(\frac{y}{L}\right)$
• B. $F_{2}\left(1-\frac{y}{L}\right)+F_{1}\left(\frac{y}{L}\right)$
• C. $\left(F_{1}-F_{2}\right) \frac{y}{L}$
• D. none of these

Answer 1

Answer: (A)

Net force on the $\operatorname{rod}=F_{1}-F_{2}$
As mass of the rod is $M,$ so acceleration of the rod is
$a=\frac{\left(F_{1}-F_{2}\right)}{M}$
Now considering the motion of part $A B$ of the rod [whose mass
is equal to $(M / L) y]$, then the equation of motion is
$F_{1}-T=\frac{M}{L} y \times a$
where $T$ is the tension in the rod at $B$.
or $F_{1}-T=\frac{M}{L} y \times\left(\frac{F_{1}-F_{2}}{M}\right) \,\,\,\,\, (Using (i))$
or $T=F_{1}\left(1-\frac{y}{L}\right)+F_{2}\left(\frac{y}{L}\right)$
Second method: To calculate tension at $B$ we can also consider the motion of the other part of the rod $i . e ., B C .$ Then the equation of motion will be
$T-F_{2}=\frac{M}{L}(L-y) \times a$
or $T=F_{2}+\frac{M}{L}(L-y) \times \frac{\left(F_{1}-F_{2}\right)}{M} \,\,\,\,\, (Using (i))$
or $T=F_{1}\left(1-\frac{y}{L}\right)+F_{2}\left(\frac{y}{L}\right) $