Question

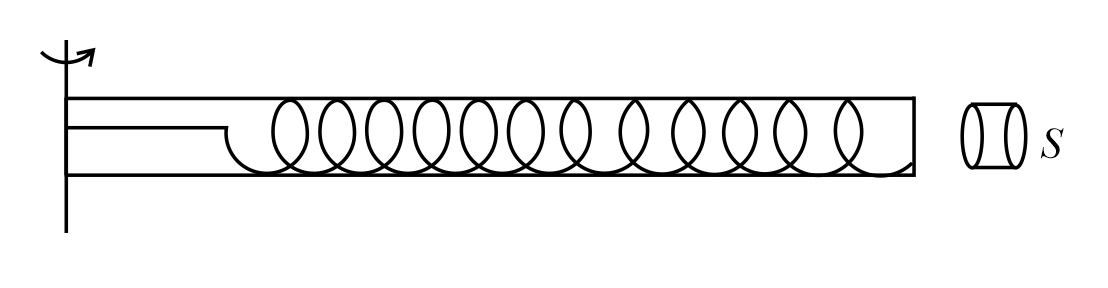
A rod of length $l = 2\,m$ is maintained to rotate with a constant angular velocity $\omega =1\, rad\, s^{- 1}$ about a vertical axis passing through one end (diagram). There is a spring constant $k=1\,N\,m^{- 1}$ which just encloses rod inside it in natural length. One end of the spring is attached to the axis of rotation. $S$ is a sleeve of mass $m=1\,kg$ which can just fit on rod. All surfaces are smooth. With what minimum kinetic energy (in $j$) sleeve should be projected so that it enters on the rod without jerk and completely compresses the spring.

Answer 1

For entering without jerk $v _{2}=l \omega_{0}=2\, m s ^{-1}$
Using work-energy theorem on the sleeve after entering in the frame of rod

$W _{\text {spring }}+ W _{\text {centrifugal }}=\Delta K$
$-\frac{1}{2} k l^{2}-\frac{1}{2} m \omega^{2} l^{2}=0-\frac{1}{2} mv _{1}^{2}$
$\Rightarrow v _{1}^{2}=8$
Now, $K =\frac{1}{2} m \left( v _{1}^{2}+ v _{2}^{2}\right)=6$