1. Tardigrade
  2. Question
  3. Physics
  4. A rod of length 50 cm is pivoted at one end. It is raised such that if makes an angle of 30° from the horizontal as shown and released from rest. Its angular speed when it passes through the horizontal (in rad s-1) will be (g = 10 ms-2)

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

Q. A rod of length $50\,cm$ is pivoted at one end. It is raised such that if makes an angle of $30^\circ$ from the horizontal as shown and released from rest. Its angular speed when it passes through the horizontal (in $rad\, s^{-1}$) will be $(g = 10\,ms^{-2})$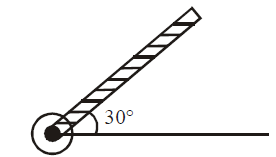Physics Question Image

JEE MainJEE Main 2019System of Particles and Rotational Motion

Solution:

Work done by gravity from initial to final position is,
$W = mg \frac{\ell}{2} \sin30^{\circ} $
$ = \frac{mg \ell}{4} $
According to work energy theorem
$W = \frac{1}{2} I \omega^{2} $
$ \Rightarrow \frac{1}{2} \frac{m \ell^{2}}{3} \omega^{2} = \frac{mg \ell}{4} $
$ \omega = \sqrt{\frac{3g}{2\ell}} = \sqrt{\frac{3\times10}{2 \times0.5}} $
$\omega = \sqrt{30} $ rad / sec

Solution Image