Q.
A rod of length $1000 \, mm$ and coefficient of linear expansion $\alpha=10^{-4}$ per degree is placed symmetrically between fixed walls separated by $1001\, mm$. The Young's modulus of the rod is $10^{11}\, N / m ^2$. If the temperature is increased by $20^{\circ} C$, then the stress developed in the rod is (in $N / m ^2$ )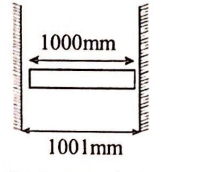
Mechanical Properties of Solids
Solution: