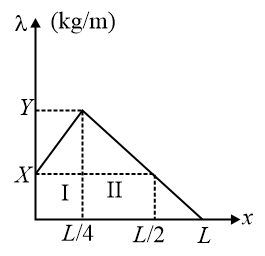
Q.
A rod has non-uniformly distributed mass $M$ over its length $L$ . Its linear mass density variation with distance $x$ from the left end is shown in the figure. From this information, we can conclude that the centre of mass of the rod,
NTA AbhyasNTA Abhyas 2022
Solution: